線形回帰について ーデータクレンジング編その②
線形回帰のデータクレンジング編その①の続きです。
前回は、
ざっと欠損値の確認、及び外れ値の処理について、確認した。
外れ値をquantileで削ることで、幾分か分布が緩やかになった。
もう一度その分布をみておく。

いい感じですね。
そして、再度、クリーンになった(ハズ)のデータの統計量を再度確認。
data_cleaned.describe()

この統計量の各項目について、散布図で示してみる。
具体的には、値段と走行距離 値段と排気量 値段と年式 の3パターン。
それぞれ見てみると…
plt.scatter(data_cleaned["Year"] , data_cleaned["Price"]) plt.title('Year and Price')

plt.scatter(data_cleaned["Price"] , data_cleaned["Mileage"]) plt.title('Mileage and Price')

plt.scatter(data_cleaned["EngineV"] , data_cleaned["Price"]) plt.title('EngineV and Price')

どれも、線形性を持っている!!とは十分に言えない…(曲線的)
そこで、対数変換を行う。
対数変換=指数分布において、対数変換を行うと、直線的なグラフになる。
log_price = np.log(data_cleaned["Price"]) data_cleaned["log_price"] = log_price



若干微妙なやつもあるが、まぁさっきのよりかは直線的だ。
では、ここで、線形回帰の特性について記載する。
①線形性であること→対数変換したんでOK
②内相性がないこと
③正規性と同分散性があること→対数変換したんでOK
④自己相関性がないこと→これは時系列データではないのでOK
⑤多重共線性がないこと→それぞれの変数が関係しているか?ということで、これは怪しい…
この5つのどれかを持っているとき、
線形回帰は使わないほうが良い。
この⑤の奴が今回ちょっと危ない。なぜなら、さっき見た、値段に対して、年式・排気量・走行距離って
明らかに多重共線している気がするからだ。
ここで、では実際にどれくらいの多重共線性を保有しているのか、について調べる。
from statsmodels.stats.outliers_influence import variance_inflation_factor variabels = data_cleaned[["Mileage" , "EngineV" , "Year"]] vif = pd.DataFrame() vif["VIF"] = [variance_inflation_factor(variabels.values , i) for i in range(variabels.shape[1])] vif #実行結果は↓
通常、多重共線性の値は>5ならOK。
それ以上なら多重共線性の事があるので、省く、が正しい。
ここでは、まぁいったんYearを省いておく。

続きは次回で!
線形回帰について ーデータクレンジング編その①
今日はPythonの実装のアウトプット。
まだまだ知らないことがたくさんあるので、そこは、勉強勉強。
今回のメインテーマはデータクレンジング。
主に2点ある。
①欠損値の処理
②外れ値の処理
について、学んだのでそれをおもむろにアウトプット。
今回扱うデータセットは車の価格の予測モデル。
当然目的変数は車の価格になるわけだが、
色々外れ値も多そう。

思いっきり最大値と平均のPriceがかけ離れている、そのほかの数字も
若干怖い。
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression as LR
from sklearn.preprocessing import StandardScaler
from sklearn.feature_selection import f_regression
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
data_csv = pd.read_csv("1.04. Real-life example.csv")
data_csv.isnull().sum()
ここまでは問題ない。
このisnullで返ってきた結果が、こちら。

やっぱありました。
ここで、
data_csv.describe()
で統計量を確認すると、データ数が4345であることを確認。

この場合全データに対して欠損値が5%以下なのでそのまま削除。
data = data.dropna()

ここからがなるほど、と個人的には思った点。
じょうきのとおり、外れ値があるのでは?とまず統計量を見て勘繰る。
そこから、
実際にグラフにしてみると一目瞭然だった。
sns.distplot(data["Price"]) #実行結果は↓

いやいや!正規分布どころか、指数関数やん!かい二乗分布やん!
そこで、
外れ値を削除するべく、新しいメソッドを学んだ。
これは今後も使えそう。
q = data["Price"].quantile(0.90) data_q = data[data["Price"] < q]
そう、quantileという関数である。
この0.90という数字は全体の90%の所の値を単数として拾ってくる、というもの。
そこから、二行目の通りに条件を作ってあげれば、

かなり外れ値の分布は収まってくれるようになった。
こうやって、他の変数についても同様に削除していく。
この続きは次回。
統計学が分かるー回帰分析・因子分析編ー
今日は午前中からpythonのコードに悩まされた…
いかにモデルの構築よりも、
データ加工の方が大事かがよくわかった…
では、今日もさらっとアウトプット。
本日はこちらの本の3章をアウトプット。
前回のハンバーガーのアウトプットがへぼすぎるので、
ちょっと自分なりに見やすいように改良を行います~。

第3章 その相関係数は有意であるのか?ー無相関検定ー

もはやこれで終わり、になってしまうんだが笑
一応まとめておく。
無相関検定とは、その相関係数(偏差平均÷標本標準偏差A÷標本標準偏差B)の値は、
一体どのくらいのモノなんだ?ということを示したもの。
この表の中の標本は20件ほどの為、恐らくT分布表を使って、
有意水準5%ないし、1%の時の、信用区間を調べ相関係数の値が
相関しているといえるのか(帰無仮説の棄却)、
相関していない(帰無仮説の採択)をジャッジする。
では、4章でお会いしましょう。
コロナショック・サバイバル
だいぶ暖かくなってきたな。
あたたかい、のか、あったかい、のか…
俺はどちらかといえば、
あたたかい、って呼んだ方が丁寧な気がする。

今日はコロナショック・サバイバルの本を読んだので、
そのまとめ、を記載します。
思いっきりまとめなんで、ネタバレしまくりボンバーYeahです。
なので、見たくない人は見ないほうがいいかな。
自分のアウトプットとして、書きます。
速攻で読んだ後、メルカリで出品したからねw
まずは全体のまとめから書いて、その後、
各章ごとにアウトプットをしていきます。
全体のまとめ
コロナの影響で経済危機にグローバル単位で大きなダメージを受けている。
でも、これは破壊的イノベーション始動の契機にもなりうる。
それは、大中小企業、どのフェーズの会社においてもそうで、
現に、Zoomなどのツールを使うことで、意外とリモートでもできたり、
コスト面においても無駄な出費というのは抑えられている。(はず?)
ここに破壊的なイノベーションのきっかけが隠れている。
耐用年数が過ぎているにもかかわらず、30年にもわたって続けてきた古典的な日本経営を今、DX(デジタルトランスフォーメーション)によって変えれば、
来るポストコロナにも耐えうる組織形成にも臆することはないだろう。
個人的な感想としては、かなり共感する部分が多かった。
また、冨山さんのJALでの実体験に基づいた記述もあり、
とても興味深く、その際に培った修羅場経験がいかに大事であるか、更には
危機的状況化において、リーダーシップはどのようにあるべきなのか、を
箇条書きにして記載いただいている。
猛スピードで書き上げた、割にはといっては失礼だが、全体的にかなり入りやすい内容になってました。
では、各章の簡単なアウトプット。
第1章 L型→G型→F型へ
ここでは、L型(ローカルに根付いたサービス)、G型(グローバルに根付いたサービス)、
F型(金融に根付いたサービス)のそれぞれの関係について述べていた。
まず、今回のコロナのダメージは、
L型→G型→F型の順番で影響を受け、(筆者は現段階はL型とG型の段階にきていると記述)
国内のGDPの7割がL型のサービスで展開している日本にとって、いかに大きなダメージを受けたか、がわかる。(ちなみに、リーマンショックの時は逆から)
L型の一例 → 観光業・宿泊業・飲食業
G型の一例 → 製造業(電化製品等)・自動車製造業・住宅
F型の一例 → 銀行・VC
L型のダメージは大きいが、これから恐らく、G型の影響も出始める。
なんとしても、G型までに食い止めないと、回復に時間がかかる
第2章 企業・人・政府が生き残るキー
歴史を見たとき、日本は30年の間にいくつかの危機を経験している。
バブル崩壊や、山一證券・長銀の破綻、東北大地震による原子力発電の崩壊など、
様々な危機を経験し、その一つ一つに政治・経済・産業の大きな転換を迎えている。
下記の条件の企業(ないし人・政府)は生き残る可能性が高い
①手元流動性の高さ=現金残高が多くある
②金融機関との信頼関係
③稼ぐ力(営業のキャッシュフローの高さ=PLは危機下では捨てる)
④自己資本の厚み
当然といえば、当然なんだが、なかなかできないでいる企業は少ない。
修羅場経営の心得
①想像力→最悪の想定をし、周りには最善の対策メニューの準備を指示
②透明性→危機下では、会社にとってBadNewsこそ、とても重要
③現金残高→とにかく使える手は使って、とにかく手元にキャッシュを多く持つ
④捨てる覚悟→優先順位をつけるトリアージ経営
⑤独断即決→危機下においては独断が強い。修羅場経験豊富なプロだけで決めるべき
⑥タフネス→たとえ、だれかを傷つける対策になっても、いかなる批判にも耐える覚悟
⑦資本の名人→2種類の資金が必要。1つは資金繰り用。もう一つは売上減少の補填用
⑧ネアカ→理屈通りにやって、できなかったらしょうがない精神を持つ
べからず経営
① 見たい現実しか見ない経営
②精神主義に頼る経営
③人望を気にする経営
④祝儀に頼る経営
⑤敗戦時のアリバイ作りに走る経営
⑥現場の実態をありのままに知らない経営
⑦条理に流される経営
⑧空気を読む経営
3章 危機で会社の基礎疾患がわかる
大企業:
稼ぐ力が落ちた。背景には日本的経営をずっと30年続けてきたこと
集約型においては大きな力を発するが、今回のコロナのような危機的状況になると、
脆くなる。
中小企業:
封建的経営にある。かまどの灰まで我のモノ経営では、会社の新陳代謝が生まれず、
結果として、最悪の事態を招いてしまう。
4章 ポストコロナを見据えて
このコロナの影響で抜本的な会社のトランスフォーメーションがしやすい状況になった。
今までの既得権益では太刀打ちできない。
破壊的危機の終わりは破壊的イノベーションの始まりであるため、
一時的にはへこんだとしても、AIベンチャーやその他シェアリングサービス企業にも、
チャンスがある。
そのチャンスを逃さない様に、リーダーは常に対策、を練り続ける必要がある。
こんな感じだ。
この記事を見て頂いたらわかるが、全体的に2章のボリュームが大きい。
一番伝えたかった部分なのだろうな、という印象を受けた。
では、また!
分散分析【1要因】
さて、今回も、アウトプットとして文字を書きます。
あまり時間がかけれないんで、サクッと行こか~。
今日もハンバーガー本の第6章でのアウトプット。

分散分析について
T検定においては、標本とできるものは2種類だけしかできない…
そこで、分散分析という方法を使用する。
これは、3つ以上のものの分散を分析することによって、
全ての組み合わせに差があるのか、それとも、少なくとも一つの組み合わせには、
差があるのか?を分析してくれる。
例えば、3店舗のハンバーガーショップがあったとして、
それぞれのショップのハンバーガーをランダムに声をかけた60人に食べてもらって、
それぞれを点数で表してもら。といったときに有効。
その場合、
帰無仮説は「それぞれの味に点数が影響はされない」
対立仮説は「少なくとも1つの組み合わせでは味が点数に影響される」になる。
群間のずれ
さっきのハンバーガーショップの例で行くと、
例えば、3店舗のハンバーガーの点数の平均が80点だったと仮定する。
その内、A店の平均は60点だったとする。
単純に20店のずれ、がある。
これを群間のずれという。
群内のずれ
一方で、A店の平均から、どれだけずれているかということも抑えておかないといけない。
この「A店の平均からのずれ」の事を群内のずれ、という。
では、実際に群間のずれ、群内のずれについて計算を行っていく。
ずれっているのは平方和っていうらしい
この「ずれ」には正式名称があって、正しくは平方和というらしい。
この平方和の式は
(データ - 平均)の二乗の総和で求められる。
そう、分散の時のあれ、である。
その為、この公式を使って、群内の平方和は
(データ - 平均)の二乗の総和+(データ - 平均)の二乗の総和+(データ - 平均)の二乗の総和…
で求められる。
それぞれの平方和はもし、標本分散がわかっていたら、
標本分散 × データサンプル数 で求められる。
全体の平方和も上記の
標本分散 × データサンプル数で求められる。
さぁ、ここで問題なのが、群間の平方和である。
こいつだけがなぜか下記の公式を取る。
(群内(それぞれのデータの中の)の標本平均 - 全体平均) × サンプル数 の総和
である。
わけがわからんが、何しかこれで求められるみたい。
次に、自由度と分散分析表について書く。
分散分析表について

こんなやつの事。
ここで新しい、文字がいくつか出てきた。
こちらの分布表を使うと、F値(F分布表で使う値)がとても分かりやすく計算できるので、
活用できそう。
自由度について
まず、群間の自由度については、
サンプルデータの数 - 1 したものだ。
上の群間の自由度の場合、3つの標本があったということ。
群内は、その3つの標本のそれぞれのデータから-1ずつ引いたものになる。
例えば、16 -1 、18 - 1 、11 -1 、の様に。
最後の全体、の自由度については割愛する。
んで、平均平方は単純に、群間の値を群内で割ったものになる。
そして、更にF値については、群間の値を群内で割ったものになる。
統計学【T検定】対応あり
対応あり?対応なし?
今回もこちらの本で勉強させていただきました。

では今日は第5章について。
前回と同じT検定の続きではあるが、今回は、「対応あり」について!
この対応あり、対応なしってのはいったいなんだ?
つまるところ、この対応あり、というのは
「その前後で比較することに意味がある」ということを言うらしい。
例えば、A子さんに2種類のハンバーガーを食べてもらって、どっちがおいしいか
数字を付けてもらう、とする。
その時、Aのハンバーガーの点数からBのハンバーガーの点数を引くことは
とても有意的な数字になる。
この状態をどうやら対応ありというらしい。
対応ありバージョンと、対応なしバージョンのTの値の求め方がちょっと違うので、
公式を書いておく。
対応ありバージョン
T = (標本平均A - 標本平均B) ÷ √標本分散 ÷データ数-1
対応なしバージョン
T = (標本平均A - 標本平均B) ÷
√不偏分散 ÷ 標本データA-1 + 標本データB-1
× 標本データA + 標本データB
そして、いつもの様にこのTの値が出たらT分布表を使って、
ある信頼区間の中の値を見て、帰無仮説・対立仮説が採択・棄却なのかを
ジャッジする。
統計学【t検定】対応なし
T検定について
今日はT検定について学んだことをアウトプットしてく…
とても読みやすく、分かりやすい…こちらの本のアウトプットです。

今日はこの本の第4章の内容!
これから、日々学ばせていただいたことをこのブログに勝手に載せていこうと思います!
では始めます!
母集団が把握できない、不明なことは多い。
そこで、標本をランダムにとってきて、そこから、推定母分散や、
信頼区間といったものを決めていく。
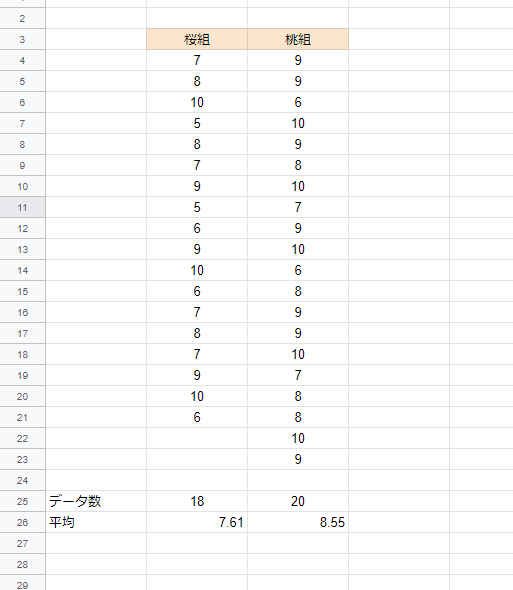
例えば、この表は2クラスの国語の点数をまとめたもの。
桃組には国語の専門の先生が教えたらしい。
ここで、T検定を行う。
帰無仮説→担任が、国語の専門家だろうが、テストの点数に影響はない。
対立仮説→担任が国語の専門家だから、テストの点数に影響する
実際は影響あったのかな??
こんな時に、
・標本がまず少ないことと、
・母分散がわからないので、T分布を使用って話らしい。
(ちょっと計算がめんどくさいので、割愛しますw)
桜組と桃組の平均差の信頼区間を調べる
そもそも、信頼区間とは…
ある確率で(95%とか99%とかが多い)母平均を含んでいるような範囲の事。
ざっくり、こっからここまでにあるでしょ!をちゃんと数値化したって感じかな…
一応公式は、
信頼区間 = 標本平均 ± t × 標準誤差
で求められます。
さくら組と桃組の平均の差は-0.94。
この-0.94ってどれくらいなんか?が気になるところ。
けど↑の公式はあくまで標本が1つの場合…
2つ以上あったときはこの公式
平均の差の信頼区間 = (標本平均A - 標本平均B) ± t × 差の標準誤差
で求められる。
いやいや、差の標準誤差って何?って話。
なんてことはない。
√(不偏分散 ÷ 標本Aのデータ数) + (不偏分散 ÷ 標本Bのデータ数)
で求められる
んで、この不偏分散ってのは、
母分散がわからん時に、推定で分散を出しましょうってやつ。
(データ- 平均)2乗の総和 ÷ データ数 -1
で求められる
最後のtについては、
今回例えば、95%の信頼区間で、って話になったとしたら、
T分布表ってのを見ながら、確認していくらしい。
↓こんなやつ
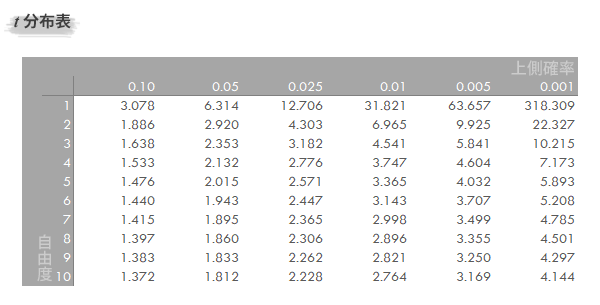
ここでいう「自由度」てのは二つの標本があった際にそれぞれを-1して足した
数字の事を言うらしい。(上の桜、桃の例えで行くと、17 + 19 = 36)
写真には端折られているけど、該当する自由度から、信頼度(今回なら0.05)の所に書かれるであろう数字がtに入る数字となる。
これで全てそろったので、
信頼区間95%の確率で母集団が入ってくる値がわかる。
この時、信頼区間の値に0が入ってくると、そもそも双方の評価には差は無いことが
十分に起こりえる、と解釈される。(有意な差ではない)
とだらだら書いたが、実はこのTの数字も求めることができる
T = 標本平均の差 ÷
√{(データA- 平均)2乗の総和 + (データB- 平均)2乗の総和}
÷ {(データA数 -1) +(データB数 -1)}
÷ (データA数 + データB数)
で求められる。
んで、Tがわかったら、さっきのT分布表を見て、
自由度が○○の時Tが○○よりも大きい、熱いは○○よりも小さいことが起こる
確率は○○%です!って
いえる。